The virtuosity of the spiking neural networks in biological brains have always been intriguing to people. Truly, a single neuron is easy to understand. However, when putting an astronomical amount of them together and they start to talk to each other, the complexity quickly go beyond control.

To pave the way of gaining more understanding of such networks, this project focuses on the stochastic modeling of the network. The goal is to develop efficient algorithms that can compute the statistical quantities of any given network without performing simulations.

Mathematical model of spiking neurons

For more complete information, I would recommend this online book. It is a well written material suitable for anyone with a quantitative background interested in computational neuroscience but with basic-to-zero knowledge in neuroscience.

So a neuron looks like this. There are four basic building block:

1. The dendrites receive signals from other neurons and propagate them to the soma; and
2. the soma, which is the cell body of the neuron, collects the signals from dendrites and fires electrical signals when it receives enough inputs; then
3. the axon transmits the signal and triggers the release of neurotransmitter to the synapses;
4. the synapses, which are the gaps between the axon ends and the dendrites of next neurons, let the chemical pass on and trigger succeeding dendrites.

FUN FACT: The yellow wraps on the axon are Meylin sheath. They are like the rubber layer of copper wires. They also help to increase the speed of transmission of the electrical signals in the axon. Meylin sheaths are formed by one of the glial cells. In this study ¹ on Einstein’s brain, it is showed that there are significantly more fraction of such cells in one region of Einstein’s brain than other human brains they tested. This might be a reason for Einstein to be a genius. (But no one is really sure. Maybe without so many glial cells, Einstein would’ve already unified quantum theory and gravitation.)

Leaky integrate and fire model

You may have heard of the Nobel Prize winning model – Hodgkin-Huxley model. But here I will not introduce it. Instead let’s look at a simpler model – the leaky integrate and fire model. This model treats a neuron as just a capacitor who fires whenever it reaches a threshold voltage and leaks over time.

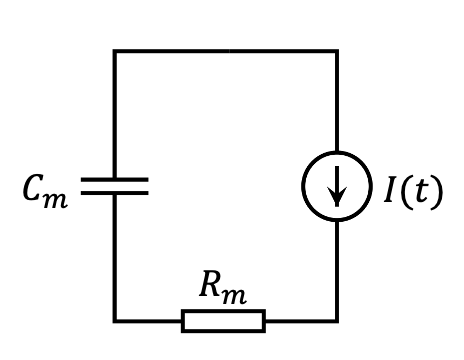
Simulation of spiking neural networks

Before diving into the theory, we really need a way to simulate the spiking neural network so that it can help us to gain insights and verify the theory. There are a lot of highly-developed simulation packages available such as NEURON, Brain, GENESIS, NEST and so on. A comprehensive list can be found in this article ²

Simulation with TensorFlow 2.0

Using those packages we can simulate this model in several lines. However, to have a basic understanding of how things work, let’s implement it using TensorFlow. But why not just a ODE solver? There are several reasons

• By using TensorFlow, we have access to the high performance infrastructure of arithmetic and linear algebra that abstract many acceleration hardwares (GPU), which are all we need; and
• the coding is just as simple as implementing a finite difference ODE solver; and
• at the same time, it becomes possible to integrate the powerful machine learning capability of TensorFlow into the post-processing of the simulation data; and
• moreover, it also enables us to develop some sort of spiking neuron layers and use that in traditional deep learning tasks.

This blog post implemented the SNN using TensorFlow 1.0 and the code is rather complicated due to the conversion of differential equation into computational graph. But with the 2.0 update, everything is just way simpler.

Single neuron

SNN_Single_TensorFlow.ipynb is the jupyter notebook for this section.

Write the differential equation in its finite difference form $$ \Delta V_m(t) = \left[ -\frac{V_m(t)-V_{\text{rest}}}{C_m R_m}+ \frac{1}{C_m} I(t) \right] \Delta t $$ Also don’t forget the firing rule $$ V_m(t^+) \rightarrow V_{\text{reset}}\,\, \text{ if } \,\, V_m(t^-) = V_{\text{thres}} $$

Translate this into python code, is just

import tensorflow as tf
# Spiking Neural Network Module, inherited from tf.Module
class SNN_IaF(tf.Module):
    # ... other code omitted ...
    # Voltage as tf.Variables
    self.V = tf.Variable(self.V_resting, name='V')

    # finite difference update step
    @tf.function
    def finite_diff_update(self, I, dt):
        # finiate difference increment dV
        dV = (I / self.C_m - (self.V - self.V_resting) / (self.C_m * self.R_m)) * dt
        # determine the spike by checking voltage with threshold
        will_fire = self.V + dV >= self.V_thres
        # update the Voltage variable
        self.V.assign(tf.where(will_fire, self.V_reset, self.V + dV))
        # return the spike information
        return will_fire

Isn’t it easy? This is because the introduce of tf.function in TensorFlow 2.0 that simplifies everything we need to do before to construct the graph.

Then the simulation is just straight-forward Euler’s method:

class SNN_IaF(tf.Module):
    # ... other code omitted ...
    
    # simulate a period of time (sim_time) given input current I_t
    def Simulate(self, I_t, sim_time, dt=0.01, clear_history=False):
        # ... other code omitted ...

        # loop of finite difference solver
        for step in range(1, total_step + 1):
            # time of this step 
            time = time + dt
            # current of this steop
            I = I_t(time)
            # update voltage
            firing = self.finite_diff_update(I, dt)

            # ... other code omitted ...

We can simulate a single neuron using the following code. It first defines a periodic square wave function and then feeds it into the model.

n = 1
# periodic square wave input current
@make_copy(n)
def I_input(t):
    if t % 300 < 150 and t % 300 > 50:
        return 10.
    else:
        return 0.

single_neuron = SNN_IaF(n, 
                        C_m=1.2, R_m=60., 
                        V_resting=-65., V_reset=-70., V_thres=35.)    

single_neuron.Simulate(I_input, 900, dt=0.5)

Here are the code for making the plots.

plt.figure(figsize=(20, 6))
plt.subplot(1, 2, 1)
single_neuron.plot_y_vs_x(0, 'I', 'time')
plt.subplot(1, 2, 2)
single_neuron.plot_y_vs_x(0, 'V', 'time', show_spikes=True)
plt.tight_layout()
plt.show()

The spiking events are marked by vertical dashed line.

A network of neurons with connections

References